Decálogo de Steve Jobs

Les comparto el decálogo de Steve Jobs, los 12 puntos que han llevado al éxito a uno de los más grandes empresarios de todos los tiempos, y que también te ayudaran a ti a convertirte en un gran hombre de negocios.

1. Haz lo que te gusta hacer. Encuentra tu verdadera pasión. La única manera de hacer un gran trabajo es hacer lo que te gusta.

2. Sé diferente. Piensa diferente.

3. Esfuerzate al máximo. Haz tu mejor esfuerzo en cualquier trabajo. No te duermas! El éxito genera más éxito. Así que mantente hambriento de éxito. Contrata a gente con pasión por la excelencia.

4. Haz un análisis DAFO.. Tan pronto como inicies/crees una empresa haz una lista escrita de fortalezas y debilidades de ti y tu empresa. No dudes en eliminar las manzanas podridas.

5. Sé emprendedor. Busca lo próximo que viene. Encuentra un grupo de ideas sobre las que hay que actuar rápida y decididamente y métete en eso. A veces el primer paso es el más difícil. Solo hazlo! Ten el coraje de seguir a tu corazón y tu intuición.

6. Comienza en pequeño, piensa en grande. No te preocupes de demasiadas cosas a la vez. Toma un puñado de cosas simples para comenzar, y entonces ve progresando hacia cosas más complejas. No pienses solo en el mañana, sino también en el futuro distante.

7. Aspira a ser líder. Posee y controla la tecnología primaria en todo lo que haces. Si hay una mejor tecnología disponible, úsala, no importa si no hay nadie más usándola. Sé el primero, y conviértelo en un estándar de la industria.

8. Enfócate en el resultado. La gente te juzga por el resultado, así que enfócate en el resultado. Sé un patrón de calidad. Algunas personas no están acostumbradas a un ambiente donde se espera la excelencia. Promociona. Si no saben de ti, no te van a comprar. Pon atención en el diseño. "El diseño no es solo como se ve o qué parece, es como funciona."

9. Pide la opinión. Pide la opinión de personas con distintos trasfondos. Cada uno de ellos te dirá algo útil. Enfócate en aquellos que van a usar tu producto. Escucha a tus clientes.

10. Innova. La innovación distingue a un líder de los seguidores. Delega, deja que otros hagan el 50% del trabajo administrativo para poder pasar el 50% de tu tiempo en cosas nuevas. Concéntrate en las creaciones importantes y en la innovación radical. Contrata a personas que quieran hacer las mejores cosas del mundo. Necesitas una cultura orientada al producto, incluso en una empresa de tecnología.

11. Aprende del fracaso. Algunas veces, cuando innovas cometes errores. Es bueno admitirlos rápidamente y seguir mejorando tus otras innovaciones.

12. Aprende continuamente. Siempre hay "algo mas" para aprender! Haz polinización cruzada de ideas tanto dentro como fuera de la empresa. Aprende de clientes, competidores y socios. Y eres socio de alguien que no te gusta, aprende a quererlo, halágalo y aprende a beneficiarte de él. Aprende a criticar a tus enemigos abierta y honestamente.

Fuente: http://www.negociosyemprendimiento.org/2010/11/las-reglas-del-exito-segun-steve-jobs.html?utm_source=feedburner&utm_medium=email&utm_campaign=Feed%3A+NegociosYEmprendimientoInversionesDineroMarketingOnlineNegocios+%28Negocios+Y+Emprendimiento%3A+inversiones%2C+dinero%2C+marketing+online%2C+negocios%29

Lecciones de Albert Einstein

1. Sigue tu curiosidad

“No tengo ningún talento especial. Solamente tengo una curiosidad pasional”

Hemos hablado sobre la importancia de este tema antes pero vale la pena repetir, y aún más si lo dice Einstein. Tu pasión debería ser tu profesión. Pregúntate a ti mismo que cosas te interesan. Para tener éxito deberías prestar mucha atención a las cosas que te da curiosidad.

2. La perseverancia no tiene precio

“No es que sea inteligente, es sólo que me quedo con el problema más tiempo.”

¿Tienes la paciencia para seguir tu rumbo aunque la vida te da golpes? O dejas un proyecto al momento cuando nubes negras aparecen en el horizonte? Einstein sabía la importancia de nunca rendirse.

3. Enfócate en el presente

“Cualquier hombre que pueda conducir con toda seguridad mientras besa a una chica guapa, no está prestando suficientemente atención al beso.”

Puedes hacer cualquier cosa, pero no todas las cosas. Einstein entendió la importancia de estar “en el momento”. Entrégate al 100% a la tarea que tienes enfrente. Energía y atención enfocada es la diferencia entre el éxito y el fracaso.

4. Comete errores

“Una persona que nunca cometió un error, nunca probó algo nuevo.”

No tengas miedo al fracaso. Equivocarse no es fracasar, los errores pueden ser útiles si aprendes de ellos, te pueden hacer mejor, más inteligente y más rápido.

5. Crea valor

“Esfuérzate no para ser un éxito, mejor ser alguien que crea valor”

No pierdas el tiempo intentando ser un éxito. Mejor pasar tu tiempo creando valor. Si creas valor vas a atraer el éxito. En mi opinión es importante descubrir cuáles son los talentos y dones de uno y poner éstos a trabajar para el beneficio de otros.

6. El conocimiento viene de la experiencia

“La información no es conocimiento. La única fuente de conocimiento es la experiencia.”

Si hay algo que he aprendido después de más de 1200 días trabajando por mi cuenta es que las discusiones están bien pero no nada mejor que tener práctica real de algo. No hay manera mejor para adquirir nuevos conocimientos. Experiencia es el alfa y omega para aprender.

Fuente: EscuelaParaRicos.net/6-consejos-de-albert-einstein/

http://negociosyemprendimiento.com/lecciones-de-albert-einstein/comment-page-1/#comment-14660

Sobre el SRI y los impuestos

• Oscar Enriquez

  El adelanto al impuesto a la renta es un robo Nathalie... Si una empresa el año pasado vendio bien, y este año ya no vende lo mismo como en el caso de mi empresa, debo pagar un impuesto calculado de acuerdo a mis ventas del año anterior... ...y como este año no voy a vender ni siquiera la mitad de lo que vendi el año anterior(por que deje de vender un producto) igual debo pagar ese valor y me dicen en el SRI que NO VA a haber devolucion ...eso es un impuesto minimo...eso es una forma de incentivar la produccion? Esa es una forma de ayudar a las PYMES? He tenido que vender activos fijos para poder pagar ese adelanto del impuesto a la renta...es eso Justo? No estoy en todo mi derecho de decir que me estan Robando? Ojala me pueda dar su punto de vista..y si me ayuda a encontrar una solucion seria mucho mejor...Ver más

  Hace 18 minutos · · 2 personasCargando...
• Ivan Chamorro

  Algo habia escuchado pero ahora que lo especifica, los ecuatorianos deberiamos estar asustados.. asustados de que el SRI quiera sacarnos de todas las formas la poca ganancia que conseguimos a punta de trabajo duro.. Entonces ...me pregunto ...los ministerios estan "impulsando" la creacion de mas PYMES en el pais, con los programas emprendeecuador, creecuador, fondepyme y otros para que el SRI tenga de donde cobrar???? para mantener el bono solidario.. que de solidario no tiene nada.. lo que ha hecho es incentivar la vagancia... lo digo yo que lo vivo en carne propia...Ver más

  Hace 2 segundos ·

Escribe un comentario...

Proyecto Pascua–Lama

IMPORTANTÍSIMO

Necesitamos ser mil personas para que el asunto sea tratado!!!

Grandísimos depósitos de oro, plata y otros minerales han sido encontrados bajos los glaciares. Para llegar hasta ellos será necesario quebrar y destruir los glaciares -algo nunca concebido en la historia del mundo- y hacer 2 grandísimos huecos, cada uno tan grande como una montaña, uno para la extracción y otro para el deshecho de la mina. El proyecto se llama PASCUA LAMA. La compañía se llama Barrick Gold. La operación esta siendo planeada por una multinacional de la cual es miembro George Bush padre... El gobierno Chileno ha aprobado el proyecto para que empiece este año. La Única razón por la cual no ha empezado aún, es porque los campesinos han obtenido un aplazamiento. Si destruyen los glaciares, no solamente destruirán la fuente de un agua especialmente pura, contaminarán permanentemente los 2 ríos de tal forma que nunca volverán a ser aptos para consumo de humanos y animales debido al uso de cianuro y ácido sulfúrico en el proceso de extracción del mineral. Hasta el último gramo de oro será enviado a la multinacional en el extranjero y ni uno le quedará a la gente a quien le pertenece esta tierra . A ellos sólo les quedará el agua envenenada y las enfermedades consiguientes. Los campesinos llevan bastante tiempo peleando por su tierra, pero no han podido recurrir a la TV por una prohibición del Ministerio del Interior. Su única esperanza para frenar este proyecto es obtener ayuda de la justicia Internacional. El mundo debe enterarse de lo que esta pasando en Chile ... El lugar por donde empezar a cambiar el mundo es nuestro lugar. Se ruega a la persona numero 1.000 que reciba este mensaje mandarlo a noapascualama@ yahoo.ca, para que sea remitido al gobierno Chileno.

No a la mina abierta Pascua Lama en la cordillera andina sobre la Frontera
entre Chile-Argentina .

Pedimos al gobierno Chileno que no autorice el proyecto Pascua Lama para proteger la totalidad de 2 glaciares, la pureza del agua de los valles de San Félix y El Tránsito, la calidad de la tierra cultivable en la Región de

Atacama y la calidad de vida de la gente afectada de la Región.

Consulta en Wikipedia: http://es.wikipedia.org/wiki/Pascua_Lama

MUCHAS GRACIAS POR TU ATENCIÓN, ... APÓYANOS !

Post Cual es la red social que mas se adapta a ti

Cual es la red social que mas se adapta a ti

AUTOR: Maestro | 15 noviembre 2010 | Visto 84 Veces | No Hay Comentarios

• Meneame 0
• Bitacoras
• Google Buzz 0
• Facebook 0
• Twitter 11

Hola a todos. Siguiendo con el tema de las redes sociales les quiero compartir una imagen que encontre bastante interesante, y con la cual podemos elegir cual es la red social que mejor se adapta a nuestro perfil y gustos. Como algunos sabemos existen una gran cantidad de redes sociales, para gustos o disgustos de muchos y siempre es bueno saber elegir cual de ellas es la mejor para nosotros.
En la imagen solo debemos seguir la secuencia respondiendo las preguntas que en cada cuadro vamos encontrando, dependiendo de nuestra respuesta llegaremos a la red que mas concuerda con nuestro interes. Entre los resultados se encuentran las principales redes del momento, asi que espero que disfruten la imagen.

Y tu a que Red Social perteneces?

Visto en: Mecongratula

¿Te gusto este artículo? ¿Quieres recibir este y mucho mas contenido en tu correo?. Suscribete, haz parte del blog y se el primero en enterarte de todo lo que se publica aqui: SUSCRIBIRME


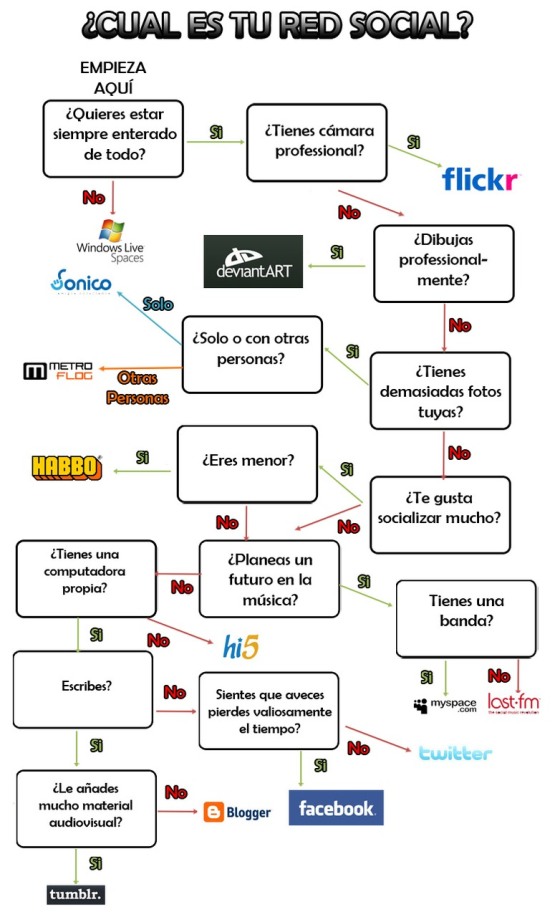
Fuente: http://www.maestrodelacomputacion.net/cual-es-la-red-social-que-mas-se-adapta-a-ti/?utm_source=feedburner&utm_medium=email&utm_campaign=Feed%3A+MaestroDeLaComputacin+%28Maestro+de+la+Computaci%C3%B3n%29

LAS FINANZAS DEL PUEBLO

El principal problema en el ámbito financiero para los pequeños y medianos productores, indígenas, campesinos, afroecuatorianos y pobladores urbano populares es que, siendo generadores de ahorros, están excluidos o tienen muy poco acceso al crédito bancario y tienen escasa incidencia en la políticas financieras locales, regionales, nacionales. La superación de este problema es un requisito indispensable para construir el desarrollo local con equidad y sostenibilidad.

Las causas centrales que originan el problema son:
a. Está en marcha un modelo con creciente tendencia excluyente y concentrada, en el que los pequeños y medianos productores, los indígenas, afroecuatorianos, campesinos y pobladores urbano populares no tienen incidencia.
b. La mayoría de estructuras financieras locales (cajas rurales, bancos comunales, cooperativas de ahorro y crédito, etc.) si bien tienen un buen posicionamiento local, aún son pequeñas, poco consolidadas y dispersas, con limitaciones técnicas en su manejo.

ALGUNOS FUNDAMENTOS
En el Ecuador hoy la mayor parte de la población, culturalmente rica y éticamente sana, sufre por la pobreza económica. Sin embargo los pobres económicos producen riqueza para otros con su trabajo, con sus productos, con sus ahorros entregados a los bancos.

Muchos pobres comienzan a entender que deben ellos mismos administrar los excedentes que producen. Vence la pobreza quien produce más de lo que consume. La diferencia entre la producción y el consumo se llama ahorro. Este ahorro debe ser monetarizado y entregado a la Estructura Financiera de cada localidad, para que sea distribuido equitativamente en préstamos destinados a la producción y a la creación de nuevos puestos de trabajo.
La mayoría de ahorristas de la EFL`s son personas pobres como las personas que reciben los créditos. Defender y utilizar bien los recursos de los ahorristas es un deber sagrado. De ahí nuestro eslogan: “La plata de los pobres para los pobres”;” La plata del pueblo para el pueblo”.
El valor del ahorro es: económico, educativo, moral (hábitos virtuosos).
El ahorro local es una palanca, que permite acceder a más recursos posibles de conseguir en CFN, CODESARROLLO, BNF y otras entidades. Apalancamientos como estos pueden invertir los flujos de la economía.
Hoy todo tiende a concentrarse en pocas manos, en pocas regiones, en pocas empresas: el dinero, la riqueza, los productos, los servicios, los trabajadores, los flujos migratorios.
Hay que descentralizar la riqueza para parar la emigración. A la población de nuestras ciudades y del norte del mundo, que a veces reciben a los emigrantes con indiferencia y hasta con hostilidades, hay que decirle: “O compran nuestros productos o reciben nuestros emigrantes”.
Esto significa invertir los flujos de la economía que concentra, la riqueza, los bienes, los servicios y las personas en Quito, Guayaquil y en el exterior.
La inversión de los flujos de la riqueza requieren de una nueva cultura y de estructuras adecuadas. La cultura del ahorro, de la programación, de la disciplina, de la equidad, vivida inteligentemente y esforzadamente por la población pobre es el requisito indispensable para el buen funcionamiento técnico de las nuevas estructuras financieras y productivas.
QUE ES UNA ESTRUCTURA FINANCIERA LOCAL (EFL)?
Una EFL es cualquier capacidad de operar ordenadamente, legal y éticamente en todo lo que se refiere al manejo del dinero, fundamentalmente el ahorro y el crédito. En otras palabras, hablamos de la capacidad de realizar intermediación financiera y construir las finanzas populares. Esto debería darse en cada comunidad rural y urbano popular, por pequeña que pueda ser.
En el Ecuador, las EFL`s toman la forma de Cooperativas de Ahorro y Crédito (que tienen personería jurídica), de Cajas Rurales, Bancos Comunales, etc. El fortalecimientos de las EFL`s exige que todas vayan madurando hasta conseguir la personería jurídica.
Entre los objetivos de las finanzas populares y de la constitución de EFL`s tenemos:
1. El combate a la usura
2. el servicio a la inversión productiva en la comunidad
3. La creación de nuevos puestos de trabajo bajo responsabilidad familiar o comunitaria
Junto a estos objetivos, que parecería puramente económicos, están el fortalecimiento organizacional, el empoderamiento individual, especialmente de la s mujeres y de los jóvenes, familiar y comunitario y el desarrollo de la cultura. Por lo tanto, una EFL es una forma organizada de educar a al gente y motivarla a ver de otra manera sus problemas y sus posibilidades.

NIVELES DE EFL`s
En orden creciente estos son los niveles según los cuales pueden ubicarse y desarrollarse la EFL`s como organizaciones que:
1. Hacen solo crédito con recursos ajenos, demostrando que tienen necesidades, ideas y potencialidades.
2. Captan ahorros locales y entregan crédito, con un coeficiente de apalancamiento.
3. Estructuran servicios de ahorro y de crédito. Cuentan con contabilidad, oficinas, horarios de atención, personal responsable, programas de capacitación, servicios informáticos, etc.
4. Se inscriben en el marco legal y consiguen la personería jurídica
5. Tienen políticas y estrategias de crecimiento, ampliación de servicios, definición de productos financieros, formación de profesionales de los dirigentes y empleados, seguimiento de la inversión, mejoramiento constante de los servicios, el control y la información.
6. Se ligan a una red local (parroquial, cantonal o provincial)
7. A su vez las redes locales se vinculan entre sí a niveles más altos, hasta llegar a nivel nacional.
La EFL`s deben:
• Estimular el ahorro
• Bajar el costo del dinero
• Financiera el desarrollo local: producción, comercio, empleo, servicios
• Ser una alternativa a la emigración
• Incluir y no excluir
• Agregar valor a la acción financiera, productiva en aspectos de organización, formación profesional, equidad, respeto del medios ambiente, participación democrática, etc.
• Descubrir la vocación y el sentido de lo local, del territorio, de cada cultura.
Todo esto una EFL sola, no logra conseguirlo. Es por tanto vital que las EFL`s se unan en redes.
QUE ES UNA RED?
Una red es un sistema de multienlaces entre entidades autónomas, pero homogéneas (en nuestro caso las EFL`s) que se articulan entre sí, sumando capacidades, potencialidades, recursos y esfuerzos para el logro de objetivos comunes y de mayor dimensión, respecto a los que cada entidad podría alcanzar en forma aislada.
TIPOS DE REDES
a. parroquiales. En la parroquia donde se vive. Unión de la EFL`s de los recintos, caseríos, anejos, barrios, comunidades, cabecera parroquial, etc.)
b. Cantorales: en el cantón donde se encuentra. Unión de redes parroquiales o de EFL`s sino hay redes parroquiales)
c. Provinciales: en cada provincia. Unión de redes cantorales o de redes parroquiales.
d. Regionales: en el espacio que abarca a varios cantones o provincias.
e. Nacional: a nivel de todo el Ecuador
Las redes deben crear beneficios para sus miembros y su constitución pretende dar valor agregado al trabajo de las familias y comunidades.
COMO CONSTRUIR REDES?
Se pueden conseguir los siguientes pasos:
1. Mapeo o Censo de todas y cada una de las EFL`s de una área geográfica, ubicando a cada una en el ámbito de la red, conocimiento informático de cuantos grupos hacen finanzas en cualquiera de los niveles antes señalados
2. Base de datos en constante actualización
3. Identificación de intereses comunes en: el desarrollo armónico del territorio, la capacitación, los servicios informáticos, el fondeo, los materiales educativos y administrativos, el marketing, la auditoria y el control.
4. Surgimiento del liderazgo local: “cabeza, corazón y manos trabajadoras”
5. Constitución de asambleas a distintos niveles.
6. Definición de normas y de instrumentos (plan de negocios, software, capacitación, etc.) comunes
7. Formación constante de dirigentes y de técnicos campesinos que asumen responsabilidades en la EFL`s y en las redes.
8. Establecimiento y oferta de servicios recíprocos, incluso financieros, al interior de las redes.
9. Obtención de personería jurídica
El reto es de ayudar a subir a cada EFL hasta el nivel más alto de sus relaciones con las redes y de cada red local hasta la red nacional.
La concepción y los contenidos son primero, las formas vienen después.
CAMPOS DE ACCIÓN DE LA REDES
Entre las principales acciones de la redes están:
• Formación ética y profesional de los directivos y personal de las EFL`s
• Aumento del número de dirigentes de las EFL`s para que haya rotación
• Concientización de las EFL`s (capacitación de los socios)
• Control, autocontrol, regularización, autoregularización de la EFL`s
• Informática
• Catálogo-código de cuentas común
• Materiales impresos comunes
• Intercambio de recursos económicos
• Incidencia política local: planes de desarrollo local, nacional, marco regulatorio de las finanzas populares
RESULTADOS CONCRETOS Y URGENTES
Las redes provinciales deben ayudar a las EFL`s afiliadas a conseguir estos re4sultados:
• Aumento de capital social de cada EFL, de socios, de captaciones (buscar donde hay, diseñar estrategias, no hacerse competencia entre EFL`s hermanas)
• Control de la morosidad
• Seguimiento a la inversión de préstamos para que se oriente a la producción y a la creación de puestos de trabajo
• Disponer de sistema informático común, sedes propias cómodas
• Genera una imagen corporativa
• Implementar seguridades en oficinas, recursos y documentos.
HACIA UNA RED NACIONAL
La nueva cultura de la Finanzas populares debe ser sostenida por estructuras fuertes. La cultura no debe entrar en conflicto con la técnica financiera. Debemos tener la fuerza de ser sistema, de no estar aislados, de tener peso político, de orientar el desarrollo local, hacia la equidad y el bienestar.
COMO LLEGAMOS A LA RED NACIONAL
Los pasos por dar pueden ser los siguientes:
1. Censo y documentación de las redes provinciales
2. Demostración de voluntad de participar por parte de cada red provincial
3. Selección de personas que se dediquen y nombramiento de una directiva provisional
4. Obtención de recursos para su funcionamiento
5. Estudio de la forma jurídica más adecuada y trámites para conseguirla.
6. Definición de misión, visión, valores, objetivos, actividades y FODA (planificación estratégica)
7. Encuentros rotativos en diferentes regiones del país
8. Definición de espacios políticos en que actuar
9. definición de normas
10. Ubicación de las finanzas populares y la economía social y solidaria en la nueva Constitución política del Ecuador (presentación de propuesta a la ASAMBLEA CONSTITUYENTE)

Ciclo virtuoso
El ciclo virtuoso que queremos construir es el siguiente:
• Socios y clientes responsables=buenas EFL`s
• Buenas EFL`s=buenas redes locales
• Buenas redes locales=buena red nacional
• Buena red nacional=fuerte incidencia política
• Fuerte incidencia política=posibilidad real de cambiar al Ecuador con justicia y en paz.

JOSÉ TONELLO
PRESIDENTE CODESARROLLO

Fuente:  http://www.codesarrollo.fin.ec/Html/finanzasp.htm

Liga a la Semifinal de la Sudamericana

L.D.U. 1 - Newells Old Boys 0: "Mamita" y su gol de Semifinal

Posted: 10 Nov 2010 09:23 PM PST

Partido sufrido, jugado con huevos por parte de ambos equipos en donde el equipo con jerarquía salió avante; la hinchada como siempre en los momentos difíciles, alienta con el alma vida y corazón y esta vez nuevamente el gol bajo de las generales, en verdad erizaba la piel estar en esas generales alentando con todo para poner nuevamente a Liga en una semifinal.
Liga desde que inicio el partido entro con todo y la busco, en el primer tiempo dos bolas en el poste y por supuesto un par de atajadas del arquero de Newells dejaron a toda una hinchada con el gol en la boca.

El segundo tiempo Bauza hizo cambios tácticos que con los cuales le gano la pulseada a Sensini, lo que sí, el cambio de Mamita por Hernán fue porque ya no daba más Barcos ya que lo dejo todo.

"Mamita" definitivamente el jugador del partido, el por qué? pues hizo el gol en el momento decisivo para que Liga pase a Semifinales nuevamente.

Pepe Pancho demostró porque es titular en Liga, que tapadas que hizo un par pero de campeonato, además la suerte del campeón en el segundo tiempo una bola en el vertical, pero que más se puede decir, es Pepe Pancho.

Jorge Guagua, incansable en la defensa, Norberto Araujo definitivamente el "Rey del anticipo", como jugo, corrió y la sudo. Diego Calderón nuevamente un muy buen partido, lo dejo todo en la cancha. Esta tripleta definitivamente la mejor defensa al momento de Liga.

Ulises, Ulises grande como siempre, un jugador eterno en Liga, salió solo por cambio táctico, para darle más movilidad a Liga con Miller.

W. Araujo definitivamente otro de los puntos altos de Liga, se lo veía en toda la cancha, jugó un partido de 10 puntos sin lugar a dudas.

Reasco jugó al nivel que viene jugando últimamente y cumplió dentro de la cancha, pero todavía no alcanza el nivel al cual estamos acostumbrados.

G. Chila jugo un primer tiempo de novela, los defensas leprosos ya no sabían que hacer con él, seguramente lo van a soñar esta noche.

Salguerio jugó un partido un poquito flojo creo yo, pero definitivamente no como los últimos partidos que lo hemos visto; todos sabemos que es un jugador desequilibrante.

C. Luna buen partido el chino las corre todas y no deja ningún balón por perdido.

Barcos, todos conocemos el nivel de Barcos, pelee todas las bolas, incansable, arriba y abajo, un guerrero Albo definitivamente.

Miller con su ingreso desequilibro el medio campo y le dio otra dinámica al partido.

EL Paraguarí entro para reforzar la defensa y cambiar a Línea de 3.

Por cierto no quiero hablar del arbitraje pero dejo mucho que desear este arbitro colombiano.

Ahora sí, los comentarios se los dejo a ustedes.

Alineación:

José Francisco Cevallos; Jorge Guagua, Norberto Araujo y Diego Calderón; Ulises De la Cruz, William Araujo, Néicer Reasco y Gonzalo Chila; Juan Manuel Salgueiro; Carlos Luna y Hernán Barcos.

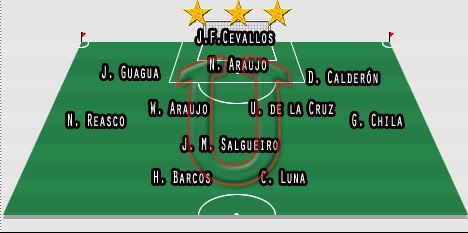
Director Técnico: Edgardo Bauza

Cambios: Ulises De la Cruz <-- Miller Bolaños; Juan Manuel Salgueiro <-- Carlos Espínola; Hernán Barcos <-- Wálter Calderón

TA: Gonzalo Chila, José Francisco Cevallos
TR: --

Goles: Wálter Calderón (79')

Jugador del Partido: Wálter Calderón

Árbitro: Óscar Julián Ruiz (Colombia)
Asistente 1: Abraham González (Colombia)
Asistente 2: Humberto Clavijo (Colombia)
4º árbitro: Imer Machado (Colombia)
Asesor: Bomer Fierro (Ecuador)

Ven y se parte de la mayor Comunidad Liguistas ... la Hinchada de L.D.U

No Olvidar:
Nuevo en Foro Liguista, Comunidad Alba: Pronósticos Albos, Albo busca Alba, Alba busca Albo, Foro Libre.

Chequea el nuevo Chat Liguista

Noticias durante el día: http://www.locosxliga.com/

Para todos los que quieran seguirnos en: Grupo Liguistas Facebook. No te Olvides de Seguirnos en Twitter:http://twitter.com/liguistas; aqui estamos actualizando información sobre LIGA cada vez que se da la misma y desde diferentes puntos.

Sígueme: http://facebook.com/chris.liguistas.
MP3's de la U, pueden ser encontrados en: MP3s de Liga
Tienes preguntas o problemas sobre el Amor? No te olvides de visitar La Mecánica del Amor

[Herman@ Alb@ deja tu comentario]

La conjetura Perelman

26 OCT 10 | La conjetura Perelman El genio, el hombre, el enigma El extraño personaje de Grisha Perelman, uno de los matemáticos más importantes del mundo. Resuelvo las conjeturas más compleas y rechaza los premios más millonarios.

El País
  RODRIGO FERNÁNDEZ

Cabello despeinado, barba hirsuta, uñas largas, mirada reconcentrada, a veces perdida, ropa vieja. Quien se tope con este personaje en la calle -cosa difícil, porque casi no sale ya de su apartamento, salvo a comprar alimentos a la tienda más cercana- seguramente lo tomará por un simple vagabundo, un bombzh. A nadie se le pasaría por la mente que ese hombre desaliñado es un genio, el mayor matemático de los últimos tiempos, que encaja en el paradigma del científico chiflado. La gente considera que efectivamente ha perdido la razón, pero no por su dudosa higiene y aspecto, sino, ante todo, por haber rechazado el millón de dólares de recompensa que le otorgó el Instituto Clay de Matemáticas (Massachusetts, EE UU) por haber resuelto la conjetura de Poincaré -uno de los siete problemas del milenio-, y se negó a recibirlo a pesar de vivir con su madre en precarias condiciones.
"No contestaré a ninguna pregunta", dice a EL PAÍS muy tranquilo, con voz cristalina, casi de niño, sin el menor atisbo de alteración. Su voz transmite cortesía y el tono es más que amable. Pero esta calma desaparece cuando tratan de ofrecerle dinero, a él o a su madre, a la que arranca el teléfono de las manos, y entonces puede gritar y mostrarse grosero, incluso con gente que le ha ayudado en su carrera. Perelman recibe esas muestras de solidaridad o de preocupación como un insulto. Grisha Perelman -su nombre es Grigori, pero él siempre ha firmado con su diminutivo ruso-, que de niño fue entrenado para ganar y recibir premios, a partir de cierto momento los rechazó todos. ¿Qué hizo que empezara a negarse a aceptar distinciones, a los ojos de todo el mundo merecidas, y comenzara a cortar relaciones y a encerrarse en sí mismo?
Un aficionado al ajedrez probablemente asociaría el caso de Perelman con el de Bobby Fischer, y quizá no anduviera muy errado: muchos especialistas consideran que ambos genios desarrollaron el mismo mal, una especie de autismo conocido como el síndrome de Aspergen. Opinión con la que, por cierto, su primer maestro está en total desacuerdo.
Antes del millón de dólares, Grisha había rechazado un premio de la Sociedad Matemática Europea y luego hizo lo mismo con la medalla Fields, llamada frecuentemente el Nobel de las Matemáticas, que debería haber recibido en Madrid en 2006, durante el Congreso Internacional.
Al comienzo, nada indicaba que su carrera iba a llegar a las más altas cimas y que -después de que el destino hubiera permitido que triunfara en la ciencia a pesar de los numerosos escollos que un judío como él encontraba en su camino en la antisemita Unión Soviética- terminaría en tragedia -para el mundo científico, al menos-, en el abandono de las matemáticas y en el encierro en sí mismo. Encierro que es prácticamente total, pues Grisha ya no se comunica con nadie, a excepción de su madre; se niega a conceder entrevistas, no responde si a uno se le ocurre ir a verlo y tocar a la puerta de su apartamento, e incluso ha roto todos los vínculos con la mayoría de sus antiguos colegas y maestros.
Grisha se refugia del mundo en Kúpchino, un barrio en el sur de San Petersburgo donde el metro muere. Construido en los años sesenta del siglo pasado, Kúpchino es un típico suburbio dormitorio. La gente que vive cerca de la casa de Perelman -un edificio tipo de nueve plantas-, los que trabajan en las tiendas adonde suele ir, ahora le reconocen. Muchos cuando lo ven sacan sus móviles, con los que le hacen fotos; pero la mayoría se comporta como Grisha quiere: lo dejan en paz.
Perelman se inició en el campo de las matemáticas muy temprano, siendo un niño, como se acostumbraba en la época soviética. Su madre, Lubov, era una talentosa matemática a la que su maestro incluso llegó a ofrecer un puesto en el Instituto Herzen, donde él mismo enseñaba. Esto era un honor, ya que su nombramiento iba a ser difícil por dos razones: primero, porque era mujer -es decir, potencialmente madre, con lo que su consagración a la ciencia resultaba incierta-, y segundo, porque era judía.
Pero Lubov desechó entonces el ofrecimiento por la sencilla razón de que se acababa de casar y quería crear una familia. Pasó más de una década antes de que Lubov volviera a ver a su maestro. Se toparon en la calle y ella le contó que tenía un hijo, Grisha, que mostraba dotes para las matemáticas, como lo probaba su reciente participación exitosa en un concurso del barrio donde vivían, en los suburbios de Leningrado, hoy San Petersburgo. Y le preguntó qué podía hacer para desarrollar ese talento.
Garold Natanson, que así se llamaba el maestro de Lubov, llamó entonces a Serguéi Rukshín, según cuenta él mismo a EL PAÍS, entonces un joven matemático con un don especial para preparar a niños. El resultado de esa conversación fue que Grisha ingresó en 1976 -recién cumplidos los 10 años- en el círculo de matemáticas que funcionaba en el Palacio de Pioneros de Leningrado.
Estos centros de élite, repartidos por la URSS, eran como grandes clubes donde funcionaban numerosos círculos para niños: de matemáticas, de ajedrez, de deportes, de música... Grisha, de hecho, llegó al Palacio de Pioneros de Leningrado sabiendo ya tocar el violín, instrumento que también había estudiado su madre, que era profesora de matemáticas en una escuela.
Como recuerda Rukshín, que en esa época tenía solo 19 años, Grisha acababa de cumplir los 10 años y no era el benjamín del círculo, ni tampoco el más brillante ni el mejor en las competiciones. Y no lo fue hasta varios años después. Era bueno, talentoso, y a diferencia de la mayoría de sus compañeros, se mostraba tranquilo, callado.
Incluso para solucionar los problemas era introvertido; prácticamente no escribía nada previo, no hacía cálculos en el papel, todo lo analizaba mentalmente hasta que obtenía la solución, que pasaba entonces a la hoja que tenía delante.
Había signos que indicaban que la solución estaba próxima: podía tirar una pelota de pimpón contra la pizarra, caminar de allá para acá, marcar un ritmo con un lapicero en el pupitre, restregaba sus muslos -los pantalones que usaba llevaban la marca de esa costumbre- y luego se frotaba las manos, además de emitir ruidos parecidos a quejas o zumbidos, que eran, en realidad, tarareos de alguna pieza musical, como Introducción y rondó caprichoso de Camille Saint-Saëns.
Al principio, Grisha no era el mejor. Pronto llegó a serlo y se convirtió en el alumno preferido de Rukshín. Éste siempre ha defendido que los niños deben concentrarse en aquello que mejor les resulta. Esta posición, dice sonriendo, ha resultado beneficiosa tanto para el ajedrez ruso como para el español. Así, aconsejó a Alexandr Jalifman, el futuro campeón mundial de ajedrez, que se consagrara al juego-ciencia y no a las matemáticas; lo mismo hizo con Valeri Sálov -el gran maestro ruso que en 1992 se mudó a España-, a quien prácticamente expulsó de su círculo matemático.
Probablemente esta concepción de Rukshín hizo que Grisha abandonara sus clases de violín para entregarse por completo a las matemáticas. Su maestro insiste en que no le obligó a dejar la música; al contrario, lo introdujo en la música vocal, a la que Perelman no estaba acostumbrado.
El que dejara de tocar el violín no significa que Grisha renunciara a la música. La verdad es que incluso hoy es una de sus pocas aficiones; le gusta la ópera, y hasta hace poco solía comprar las entradas más baratas en el gallinero del Teatro Mariínski (ex Kírov). También se le puede ver a veces en los conciertos de jóvenes cantores.
Rukshín no solo fue el descubridor de Perelman, sino su primer maestro, el que lo formó y fue su primer tutor científico. Entre ambos se creó una relación especial. Al acercamiento con Grisha contribuyó probablemente el que después de las clases en el Palacio de Pioneros, dos veces por semana, hacían juntos el trayecto en el metro hasta la última estación, Kúpchino, el barrio de Perelman. Rukshín tenía que tomar allí un tren de cercanías hasta su casa, que en ese tiempo estaba en la ciudad de Pushkin.
A los 14 años, Rukshín comenzó a darle clases intensivas de inglés, para que Grisha pudiera entrar en el colegio especializado en física y matemáticas, la famosa Escuela Número 239 de Leningrado. El inglés era el idioma extranjero que estudiaban allí, mientras que en su escuela Grisha había aprendido francés. Al final de las vacaciones, Rukshín había logrado lo imposible: que Grisha estuviera al nivel requerido, o sea, había hecho en menos de tres meses lo que los otros niños habían conseguido en cuatro años.
Grisha ingresó junto con sus compañeros del club en la famosa escuela. Se trataba de la primera vez que, en lugar de dispersar a los miembros del círculo de Rukshín en diferentes clases, los pusieron a todos en una. Así comenzaba otro experimento ideado por Rukshín -no separar a los niños superdotados-, aunque entonces ellos formaran solo la mitad del curso; hoy ya hay clases que funcionan exclusivamente con chicos especialmente talentosos para la ciencia.
El elegido como profesor jefe en la clase de estos superdotados fue Valeri Rízhik, un pedagogo innato, según asegura Masha Gessen en su libro Perfect rigor: A genius and The mathematical breakthrough of the century, dedicado a Perelman.
La idea de Rukshín de no separar a los pequeños genios generó polémica, pero finalmente se impuso; el mismo Rukshín seguiría preparándolos en el club particularmente para las olimpiadas de matemáticas. Rízhik recuerda que Perelman se sentaba al fondo de la clase, nunca hablaba, salvo cuando veía un error en las demostraciones que los niños hacían en la pizarra; entonces levantaba apenas la mano y corregía. Era un chico que se tomaba las reglas al pie de la letra, y por eso nunca se distraía.
Rízhik solía llevar los domingos a los niños de su clase a caminar por el campo o por el bosque, y en las vacaciones, a largas excursiones a otras regiones de Rusia. Grisha nunca fue a ninguna, ni asistió a los Martes Literarios que organizaba su profesor. La opinión de Gessen de que Rízhik desempeñó un importante papel como pedagogo no es compartida por Rukshín, que otorga más méritos a Nikolái Kuksa, ex oficial de submarino que protegió a Grisha durante sus estudios en la Escuela Número 239.
A pesar de sus excentricidades y de su dificultad para comunicarse con otros, Perelman siguió su carrera matemática con relativa normalidad, sobre todo gracias a las personas que, viendo su talento, lo protegieron y consiguieron que fuera admitido en la discriminatoria Facultad de Matemáticas de la Universidad de Leningrado, que solo aceptaba a dos judíos al año. La táctica seguida para ello fue conseguir que Perelman formara parte del equipo olímpico ruso de matemáticas, ya que sus miembros ingresaban automáticamente en la Universidad que eligieran. Grisha no solo lo consiguió, sino que logró un extraordinario resultado en las Olimpiadas de Budapest: 42 problemas resueltos de un total de 42.
Perelman vivía en su propio mundo, ignorando la realidad del mundo exterior, que creía que era justo y que funcionaba como debía, siguiendo reglas claras. Nunca se interesó por la política, tampoco por las chicas, ni se enteró de que la sociedad soviética era antisemita. Su madre, sus profesores y entrenadores se preocuparon de protegerle de esa realidad exterior, de solucionar sus problemas y de garantizar que pudiera dedicarse exclusivamente al mundo de las matemáticas. Fue gracias a ellos -Rukshín, Kuksa, Rízhik, Alexandr Abrámov en el colegio y las competiciones; Víktor Zalgaller, Alexandr Alexándrov y Yuri Burago después- como Perelman pudo terminar la facultad, obtener su doctorado, ganar becas en el extranjero, dar charlas y enseñar.
A los 29 años, estando en EE UU, la Universidad de Princeton mostró interés por contratarlo como profesor asistente, pero él se negó a presentar un currículo; dijo que si lo querían, que le dieran un puesto de profesor titular. No lo hicieron y lo lamentarían.
Perelman fue a Princeton a principios de 1995 a dar una conferencia sobre su prueba de la Conjetura del alma (Soul conjecture) y para entonces se había convertido ya en el mejor geómetra del mundo. ¿Por qué esas exigencias, para qué querían un currículo suyo si habían asistido a sus conferencias? Encontraba absurdo que le pidieran datos sobre su persona. Tampoco aceptó una propuesta para ser profesor titular en Tel Aviv.
De vuelta a San Petersburgo ese mismo año, terminado su Miller Fellowship en Berkeley, Perelman regresó a casa con su madre y al laboratorio de Burago.
Grisha parece haber desarrollado una especie de alergia a los premios a mediados de los noventa. En 1996, la Sociedad Matemática Europea celebró su segundo congreso cuatrienal en Budapest, en el que instituyó premios para matemáticos menores de 32 años. Burago, Anatoli Vérshik, entonces presidente de la Sociedad Matemática de San Petersburgo, y Mijaíl Grómov, el introductor de Perelman en Occidente, presentaron a Grisha, cuya candidatura salió victoriosa. Pero éste, al enterarse, dijo que no quería el premio y que no lo aceptaría; incluso amenazó con montar un escándalo si anunciaban que él era el ganador.
Extraña actitud en una persona que había sido entrenada para ganar olimpiadas, y por tanto, premios. Nunca en su época de competidor había dado indicios de oponerse a los galardones. Más aún, sus fracasos -dos seguidos- fueron los que, según Rukshín, hicieron que Perelman se pusiera las pilas y trabajara duro para triunfar y convertirse en un auténtico científico.
Además, ya como matemático puro y duro, recibió a principios de los años noventa un premio que le otorgó la Sociedad de Matemáticas, que aceptó gustoso.
Todo apunta a que empezó a irritarle la idea de que otra persona pudiera juzgar su trabajo, cuando él se consideraba ya el mejor del mundo. Además vivía bajo una enorme autoexigencia, que le llevaba a considerar que no era merecedor del premio en cuestión, entre otros motivos, porque no había completado su trabajo todavía.
Esta conciencia de su superioridad unida a su rigidez moral -modelada en torno a la figura ideal de Alexándrov, con la exigencia de decir siempre la verdad y solo la verdad- es lo que, según quienes le conocieron, le lleva a rechazar ese premio y otros posteriores.
Paralelamente comienza a autoaislarse de la comunidad científica, aunque participa en actividades matemáticas con niños. Pero en 1996 deja de contestar a los correos electrónicos de sus colegas norteamericanos y prescinde de discutir sus proyectos. A partir de ese momento, nadie sabía en qué estaba trabajando Perelman, aunque seguramente fue cuando comenzó su asalto a la conjetura de Poincaré.
Que Grisha no había desaparecido del todo quedó claro cuatro años más tarde, cuando el matemático norteamericano Mike Anderson recibió un correo electrónico en el que el genio ruso le planteaba algunas dudas sobre un trabajo que este acababa de publicar.
Dos años y medio después se confirmó que Grisha no era de esos talentos prometedores que de pronto se paran y quedan empantanados. El 2 de noviembre de 2002, Anderson recibió, al mismo tiempo que un puñado de matemáticos, otro correo de Perelman en el que informaba de que había colgado un nuevo trabajo en Internet.
De hecho, se trataba de la demostración de la conjetura de Geometrización y de la de Poincaré, aunque él no lo especificaba. Anderson leyó el trabajo, comprendió su importancia e invitó a Perelman a EE UU, cosa que, para su sorpresa, éste aceptó. Al mismo tiempo, envió correos a otros matemáticos llamándoles la atención sobre lo que Grisha había publicado en la Red.
Un año más tarde, el 10 de marzo de 2003, Perelman colgó una segunda parte de su trabajo, mientras hacía los trámites para el visado que le permitiera viajar de nuevo a EE UU. En Norteamérica, Perelman dio magníficas conferencias y comentó a un colega que creía que pasaría un año y medio o dos antes de que se comprendiera la demostración expuesta en su trabajo.
Al mismo tiempo, comenzaron los problemas. The New York Times publicó dos artículos en los que escribía que Perelman había asegurado que había probado la conjetura de Poincaré e insinuaban que lo había hecho para ganar el millón de dólares de recompensa anunciado por el Instituto Clay. Para Grisha, esto, además de ser completamente falso, era un insulto. La verdad es que había empezado a trabajar en Poincaré mucho antes de que el Clay seleccionara los siete problemas del milenio y nunca había tenido especial interés por el dinero.
Perelman rechazó las numerosas ofertas que le hicieron para quedarse en EE UU y regresó a San Petersburgo en abril de 2004. El 17 de julio colgó la tercera y última parte de su trabajo. Si la primera era de 30 páginas y la segunda de 22, esta tenía apenas siete.
Paradójicamente, el hecho de que Grisha colgara su prueba en Internet y se negara a publicarla en una revista especializada -como era la costumbre y una de las condiciones del Clay para dar el millón de dólares- impulsó una amplia discusión sobre su trabajo, abierta y pública, que se desarrolló en seminarios y conferencias especiales.
Algunos matemáticos acometieron la tarea de explicar los trabajos de Perelman y su demostración de las conjeturas de Poincaré y Geometrización, pero también hubo otros que trataron de robarle los laureles y se autoproclamaron como los verdaderos artífices de la solución. Al final tuvieron que dar marcha atrás y reconocer el mérito a Grisha, pero todo esto, así como la demora del Instituto Clay en reconocer la prueba, unida a la indiferencia de sus colegas rusos -que no salieron en su defensa cuando trataron de robarle su logro- debieron abrir una herida profunda en Grisha.
La desilusión en el mundo de los matemáticos, que él creía perfecto y puro, fue creciendo a su regreso de EE UU, al tiempo que aumentó su autoaislamiento. Hasta que en diciembre de 2005 renunció al puesto en el Instituto Steklov, donde trabajaba. Cuando lo hizo, anunció que abandonaba las matemáticas.
Al año siguiente, Perelman recibió un correo electrónico del comité encargado del programa del congreso mundial en el que deberían entregarle la Medalla Fields, invitándole a dar una conferencia con motivo de esta entrega. Pero ni siquiera respondió. Y cuando el director del Steklov habló con Grisha, este le dijo que no había contestado porque los nombres de los miembros del comité eran secretos y él no participaba en conspiraciones.
Si puede haber cierta lógica en el rechazo al premio de la Sociedad Europea -no consideraba completado su trabajo- y en el de la Medalla Fields, que es un estímulo a los ma-, es más difícil comprender su renuncia al millón de dólares del Instituto Clay, que se entrega por solucionar un problema determinado.
Rukshín sostiene que el rechazo al dinero se debió principalmente a la profunda desilusión que sufrió al ver la injusticia de la comunidad matemática y lo que él consideraba deshonestidad, como se lo explicó a John Ball, presidente de la Unión Internacional de Matemáticas, cuando renunció a la Medalla Fields.
Lo que lo desconcertó, lo perturbó, según su maestro, no fue que el mundo fuera imperfecto, sino que el mundo de los matemáticos lo fuera también. Precisamente el mundo que se ocupa de la ciencia más exacta, donde algo o es verdad o es mentira, y donde no hay posición intermedia entre uno y otro extremo, entre correcto o incorrecto. Grisha, según sus allegados, creía que en este universo había un espacio perfecto, el altar de la matemática; él se consagró precisamente a ello y se inventó un paraíso. Y eso también falló. En esto consiste la catástrofe, y aquí, afirma Rukshín, está también la diferencia con Bobby Fischer, que no podía comunicarse con el mundo. Perelman puede: todos sus vecinos atestiguan que se comporta normalmente con ellos, que es sociable y gentil.
Rukshín explica así los sentimientos que llevaron a Grisha a renunciar al millón: "Para comprender a Perelman, imagínese que el teorema es como su hijo, que en la infancia pasó por una enfermedad grave, durante la cual no sabía si sobreviviría o no. Mientras no has demostrado el teorema, mientras continúa siendo una conjetura, es como tu hijo enfermo. Y Grisha estuvo junto a la cabecera de ese hijo nueve o 10 años, luchando por su vida y cuidándolo día y noche. Por fin, el niño sanó, creció, es fuerte y hermoso; pero te lo quieren robar y te lo secuestran. Para Grisha fue como un secuestro cuando trataron de apropiarse del resultado de su trabajo. No pudo aceptar que un teorema pudiera ser comprado, vendido o robado".
Un talento matemático  

  » Grigori Perelman nace el 13 de junio de 1966 en Leningrado (actual San Petersburgo).
» A los 14 años ingresa en la Escuela 239 de Leningrado para jóvenes talentos.
» En 1982 obtiene la medalla de oro en las olimpiadas de matemáticas como miembro del equipo de la URSS.
» En 1996 rechaza el premio de la Sociedad Matemática Europea para jóvenes matemáticos.
» En 2002 resuelve la conjetura de Poincaré.
» En 2005 renuncia a su puesto en el Instituto Steklov.
» En agosto de 2006 rechaza la medalla Fields, considerada el Nobel de las Matemáticas.
» En marzo de 2010 no acepta el premio de un millón de dólares que le concede el instituto Clay de Matemáticas.
Grisha por los puentes de Königsberg
JAVIER SAMPEDRO 

La topología, la especialidad de Perelman, tiene el más encantador de los orígenes. La ciudad de Königsberg, la actual Kaliningrado rusa, tenía siete puentes para salvar el complicado trazado del río Pregel. Cinco puentes daban a una isla interior y los otros dos cruzaban los brazos del río por otros sitios. La gente se preguntaba si sería posible cruzar la ciudad pasando solo una vez por cada puente. Y fue el gran matemático suizo Leonard Euler quien halló la respuesta.
Si llegas a la isla por un puente, se dijo Euler, tienes que salir por otro, luego la isla tiene que tener dos puentes, o cualquier otro número par. Como tenía cinco, la respuesta era no. Lo importante fue el atajo que usó Euler. Se desentendió del mapa real de Kaliningrado casi por completo y solo se quedó con un gráfico minimalista que podría servir para otras muchas ciudades, reales o imaginarias. Prefiguró así la topología, una geometría de las cualidades.
La topología se ocupa de las propiedades de un objeto que permanecen por mucho que se le deforme (sin romperlo ni abrirle agujeros). Como la A se puede deformar hasta una R, ambas letras son equivalentes para la topología. No así la B (con dos agujeros) ni la M (sin ninguno).
Un cubo tiene 6 caras, 8 vértices y 12 aristas. La operación 6+8-12 nos da la característica de Euler del cubo, que es 2. Un octaedro tiene 8 caras, 6 vértices y 12 aristas, lo que nos da una característica de 8+6-12 = 2 otra vez. Sigamos subiendo el número de caras. El dodecaedro da 12+20-30 = 2. El icosaedro da 20+12-30 = 2. Por más que aumentemos el número de caras, la característica sigue siendo 2, y esto vale también para el poliedro de infinitas caras, que es la esfera. Todos estos objetos son intercambiables para la topología: se pueden deformar unos en otros.
Como pasaba con las letras, sin embargo, los objetos con un agujero tienen una característica distinta (0). Da igual que sea una casa de vecinos con su patio, un donut (toro, en la jerga) o una taza de café: todos tienen característica 0 y son equivalentes para la topología, pero en un grupo separado de la esfera y sus acólitos. Unas gafas sin cristales representan otra clase más, con dos agujeros, como un doble toro (dos donut siameses), con característica -2.
Fue otro gran matemático, el francés Henri Poincaré, quien desarrolló sistemáticamente los fundamentos de la topología a principios del siglo XX. Su éxito fue espectacular, pero se dejó pendiente un problema grave. No logró extender del todo los anteriores principios a un mundo de cuatro dimensiones.
En nuestro mundo de tres dimensiones, los objetos sin agujeros, por muy distintos que sean, se pueden reconocer por una propiedad llamada conectividad simple. Significa que si les atas una goma elástica alrededor, siempre puedes recuperar la goma sin desatarla, solo corriéndola. Esto no pasa con un donut. Y Poincaré no pudo demostrar que lo mismo vale en un mundo de cuatro dimensiones (donde la esfera no se puede imaginar, pero sí analizar matemáticamente). Supuso que sí, y esa suposición pasó a llamarse conjetura de Poincaré. Hicieron falta cien años para que Grisha Perelman lograra demostrarla, convirtiéndola en un teorema.
Perelman no solo ha resuelto un problema que se les había resistido a los mejores matemáticos del mundo durante 100 años, sino que para hacerlo ha desarrollado unas herramientas que abren un nuevo continente a la investigación matemática. No olvidemos que, según la relatividad de Einstein, vivimos en un espaciotiempo de cuatro dimensiones. La más abstracta de las disciplinas matemáticas es ahora capaz de descubrir la forma de nuestro universo. Y ha salido gratis.

Fuente: http://www.intramed.net/contenidover.asp?contenidoID=67876&uid=202661

Momento Poetico

Te vi un punto y flotando ante mis ojos
la imagen de tus ojos se quedó,
como la mancha oscura orlada en fuego
que flota y ciega si se mira al sol.

Y dondequiera que la vista clavo
torno a ver sus pupilas llamear;
mas no te encuentro a ti, que es tu mirada,
unos ojos, los tuyos, nada más.

De mi alcoba en el ángulo los miro
desasidos fantásticos lucir:
cuando duermo los siento que se ciernen
de par en par abiertos sobre mí.

Yo sé que hay fuegos fatuos que en la noche
llevan al caminante a perecer:
yo me siento arrastrado por tus ojos,
pero adónde me arrastran no lo sé.

Fragmento de Rimas,
de G. A. Bécquer 

Ojos que nunca me veis,
por recelo o por decoro,
ojos de esmeralda y oro,
fuerza es que me contempléis;
quiero que me consoléis
hermosos ojos que adoro;
¡estoy triste y os imploro
puesta en tierra la rodilla!
¡Piedad para el que se humilla,
ojos de esmeralda y oro!

Ojos en que reverbera
la estrella crepuscular,
ojos verdes como el mar,
como el mar por la ribera,
ojos de lumbre hechicera
que ignoráis lo que es llorar,
¡glorificad mi penar!
¡No me desoléis así!
¡Tened compasión de mí!
¡Ojos verdes como el mar!

Ojos cuyo amor anhelo
porque alegra cuanto alcanza,
ojos color de esperanza,
con lejanías de cielo:
ojos que a través del velo
radian bienaventuranza,
mi alma a vosotros se lanza
en alas de la embriaguez,
miradme una sola vez,
ojos color de esperanza.

Cese ya vuestro desvío,
ojos que me dais congojas;
ojos con aspecto de hojas
empapadas de rocío.
Húmedo esplendor de río
que por esquivo me enojas.
Luz que la del sol sonrojas
y cuyos toques son besos,
derrámate en mí por esos
ojos con aspecto de hojas.
Poemas de Salvador Díaz Mirón